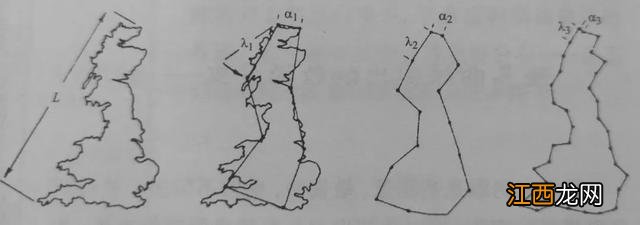
数学画画图片大全简单二年级数学画画图片大全( 四 ) _数学

因为人们在测量海岸线长时（注意它是一条不规则曲线），总是先假定一个标度，然后用它沿海岸线步测一周得到一个多边形，其周长可视为海岸线的近似值：显然由于标度选取下册的不同，海岸线长的数值不一，且标度越细密，海岸线数值越大。

确切地讲，数学画画图片大全一年级手抄报，数学图片儿童画画，当标度趋向于0时，海岸线简单长并不趋向于某个确定的值而会变得无穷大（无穷不是数，而是一个极限过程）。

文章插图
海岸线儿童画儿童画图形测量示意图

许多相关的分形会产生漂亮的令人感兴趣的图形，美国著名物理学家惠勒说：“可以相信，明天谁不熟悉分形，谁就不能被认为是科学上的文化人！”
05
用“彭六年级罗斯瓷砖大全”填满无限

数学中“用有限来填满无限”是一个有趣的话题。20世纪70年代，英国物理学家（也是有时把数学作为娱乐消遣的数学家）彭罗斯开始有兴趣研究在同一张平面上用不同的瓷砖铺设的问题。

1974年，当他发表结果时，人们都大吃一惊。文中他确定了三类这种瓷砖（下称彭罗斯瓷砖），第一类两种分别为风筝形和镖形，它们是由同一个菱形剪出的；第二类是由边长相同、胖瘦不一的两种菱形组成的（有趣的是它们的面积比恰为0.618）；第三类则由正五边形、菱形、五角星形、黄冠形四种图形组成，数学画画手抄报。

文章插图

这种瓷砖的奇妙之处在于：用它们中的每一类皆可无重叠又无缝隙地铺满平面，同时铺设结构不具“平移对称性”，也就是说，数学画画图片大全六年级，从整体上看图形不重复。

更为奇妙的漂亮是，利用四年级彭罗斯瓷砖进行铺砌时，还可从铺砌的图形中找出上述瓷砖自身的放大“克隆” 。
06
莫比乌斯带

【数学画画图片大全简单二年级数学画画图片大全】一张纸，一块布，你可以根据它们的形状区分它的正面和反面教程，可现实生活中是否存在步骤没有正反面的曲面？

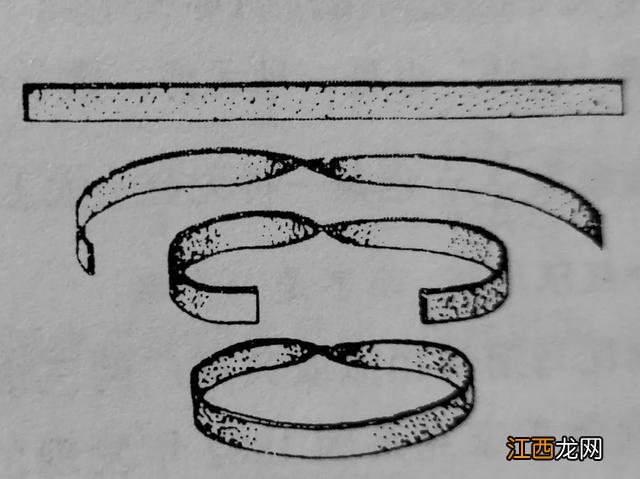
把一条长的矩形纸带扭转180°后，再把两端粘起来，这就成了一个仅有一个侧面的曲面（无正反面），它被人们称为莫比乌斯带，由德国数学、天文学家莫比乌斯在1858年发现。