3x+1的数学问题( 二 )

2022-04-24 知识百科问题数学

角谷是说，输入X=1，3，5，7，9，11，....任何一个奇数，直至无穷，经过(1)迭代，都是(1)式等于1 。
三、问题难倒了全世界的数学家
需要证明两个结论以后才有可能完成：
1、任何一个X值进入迭代以后不会回到自身，就是不会发生循环。如果发生循环，表明是一个反例，否定了角谷猜想。
2、X 进入迭代以后数值不会发散，就是不会越来越大直至无穷，而是在一个有限的范围内更替。
四，倒行逆施
由把(1)式中的

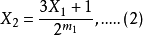
文章插图
, 在(2)式一步到位等于1的有

文章插图
形的数： 5，21，85，341，1365，5461，21845，..... 。因为这个

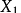
文章插图
是把(2)式反推的结果。

文章插图
在(3)式二步到位等于1的有

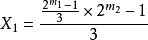
文章插图
形的数：3，13，53，113，227，909，.... 。因为这个

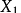
文章插图
是把(3)式反推的结果。

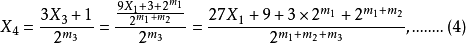
文章插图
在(4)式三步到位等于1 3的有

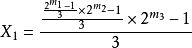
文章插图
形的数：11，17，75，301，1205，... 。因为这个

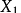
文章插图
是把(4)式反推的结果。
.............
我们可以一直进行下去：

文章插图
3x+1猜想其实就是说，无论

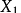
文章插图
是什么奇数值，最终会使得(5)式中分子=分母。例如，

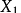
文章插图
=27，n=40时，分子=分母。
3x+1猜想反过来说就是：

文章插图
;

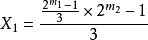
文章插图
，

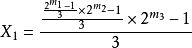
文章插图
，
可以构造一切奇数，或者说，奇数轴上每一个点，都是可以由这个数列产生的奇数覆盖。
问题进入了一个形式化的阶段
【3x+1的数学问题】这个猜想是不是递归可枚举集?下一步如何证明?是否可以利用(5)式证明猜想成立，或者证明迭代不会循环。

相关经验推荐

上一篇：猫咪养护五注意 10种适合当家猫的猫咪大全

下一篇：及时发现疾病的征兆需要定期进行体检三类人