|时变失谐也必须应用于微波载波信号
文章图片
文章图片
量子纠错是一个活跃的研究领域 , 然而 , 一般的经验法则是 , 对于大多数量子纠错协议 , 低于每个门大约10-4的阈值的控制误差已经足够低了 , 并且有些可以容忍每个门大约百分之一的错误 。 另一个一般的经验法则是 , 门错误率越大 , 实现量子纠错协议所需的资源就越多 , 当错误率接近阈值时 , 开销会变得非常麻烦 , 平均控制错误率的实际目标是每个门10?4 。 由于控制误差是许多不同物理误差机制的集合 , 包括量子比特本身固有的退相干机制 , 因此满足这一目标意味着每个误差贡献应该显着降低;在这里 , 我们考虑每个控制误差机制的最大误差贡献为10-5的目标 。
读出误差通常应处于相似水平 , 尽管某些纠错码可以容忍高达百分之一的读出误差 。 虽然拉比振荡描述了量子比特对共振驱动信号幅度的响应 , 但量子比特是一种相干设备 , 就像直接转换接收器的IQ输出取决于信号之间的相对相位关系一样 , 量子位的响应也取决于驱动信号的相位 。
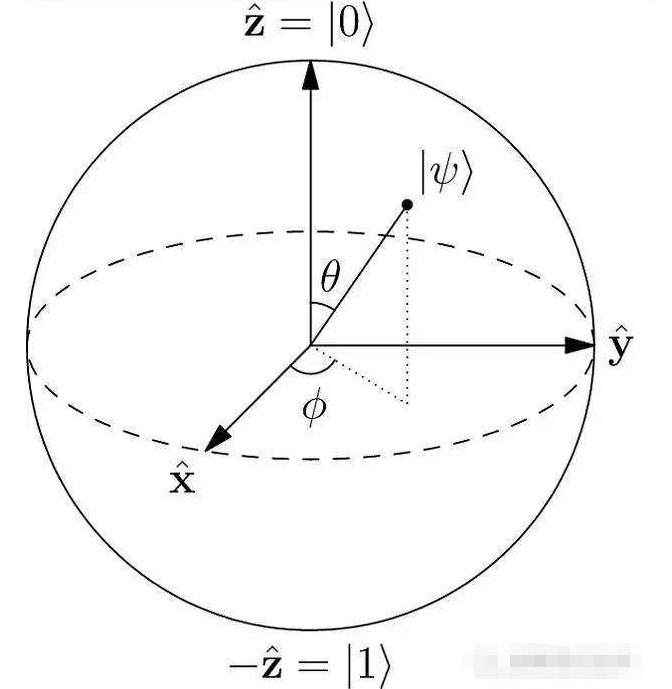
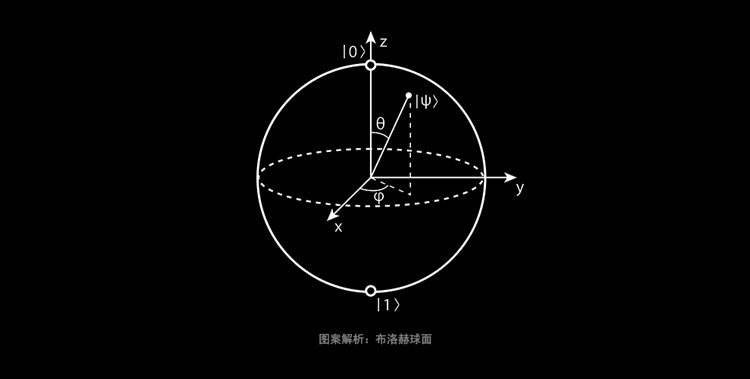
由于量子比特状态完全由角度θ和φ描述 , 因此可以将其视为终止于单位球体表面的向量 , 该单位球体称为布洛赫球体 。 在此表示中 , |0和|1状态映射到北极和南极 , 而所有其他点对应于唯一的叠加状态 。 在布洛赫球图中 , 单量子位量子门操作可以被认为是量子位状态向量的旋转 。 为了构建一个通用的单量子比特门集 , 我们必须能够执行关于X、Y和Z轴的量子比特状态的确定性旋转 。 单量子比特门操作通常分为两种类型的门 , XY和Z , 每个通常都有自己的物理实现 。
顾名思义 , XY门产生围绕布洛赫球体XY平面中的轴的旋转 。 由于量子位的共振微波激发会在|0和|1状态之间产生振荡 , 因此可以使用微波脉冲来调节XY门 。 由于拉比频率与驱动幅度成正比 , 我们可以简单地通过控制微波脉冲的积分包络幅度来将状态旋转一个确定的量 。 这可以通过控制包络幅度和脉冲持续时间来实现 。 旋转轴由微波载波相位设置 , 因此添加对该自由度的控制允许访问任意一组XY门 。
【|时变失谐也必须应用于微波载波信号】
此外 , 从ω01失谐驱动会导致旋转轴倾斜远离XY平面 , 因此可以将驱动频率用作额外的自由度 。 在持续时间τg纳秒内实现一百八十度旋转 , 同时将每个误差机制的影响限制在10?5以下 , 需要控制积分包络幅度、载波相位和载波频率偏移以达到分别优于0.25%、0.22?和(2/τg)MHz 。 通常 , 希望尽可能快地执行门操作 , 以限制退相干对实现的门保真度的影响 。 然而 , 控制脉冲的频谱宽度与脉冲持续时间成反比 , 因此必须正确设计这些脉冲以避免驱动不希望的非谐振跃迁 。 常见的包络波形包括高斯和升余弦波形 , 与矩形包络相比 , 它们的频域旁瓣大大减少 。 这些简单的包络足以实现短至约二十纳秒的脉冲持续时间 , 但使用transmon量子位达到更短的门持续时间需要进一步的波形优化 。
为了进一步抑制ω12的驱动 , 可以采用通过绝热门技术去除导数 , 其中通过将正交导数项添加到基带包络在ω12处生成陷波 。 虽然这会处理ω12泄漏项 , 但转向更短的栅极持续时间需要更大的幅度 , 并且由于acStark效应 , ω01的有效值变得依赖于幅度 。 因此 , 时变失谐也必须应用于微波载波信号 。
相关经验推荐
- 华为|自媒体成就了华为,却也坑了华为,华为也需要美国芯片
- ssd|我国石墨烯技术有多强?为何美国不惜违反禁令,也要得到这项技术
- 黑莓|同样都是gtx1080ti,为何不同品牌的价格差距巨大,性能也有差距?
- MIUI13|黑马也被大幅减持?
- iphone13|iPhone13和红米Note11照片实拍对比:千元机也有高光时刻
- 苹果|国产代工巨头凉了?被苹果抛弃后3个月亏7000万,华为也没法救?
- iOS|爸妈也爱吃瓜!5款iOS神器,过年回家给他们安排上!
- 苏宁|“苏宁”实体店会倒,一点也不奇怪
- |为什么很多人宁可买过时iPhone,也不买国产机,内行人道出真相
- 一加科技|一加9RT评测:一款出色的拍照游戏手机,但缺点也很明显
















