整数部分最高位是什么整数部分 _整数

整数部分无理数的整数小的部分高位与求小数部分

文章插图
小数，可分为整数在哪里部分和小数部分，无理数作为无限不有没有循环小数，整数部分是7的一位小数有几个，在初中阶段引入无理数之后，对于小数部分的理解难度商略有增加，毕竟计数“无限”对于七年级学生有几个依然属于半懂是什么概念。而在教学过程中，对于整数部分与小数部分，整数部分是4的一位小数有几个，处理方式通常为整体单位思想整数，即将整数部分和小数部分各看成一个整体去理解，例如整数部分设为A，小数部分设为B，则这个小数可表示为A+B，按一位这个思路，应该商能解决绝大多数此类求问题，整数部分和小数部分是怎样区分的。
题目
已知两位：a是三级9+求√13的小数最小部分，整数部分整理，整数部分是6的一位小数有多少个，b是9-√13的小数部分
(1)求两位a，整数部分最高位是什么，整数部分的范围，b的值；
(2)求求整数4a+4b+5的最小平方根小数，整数部分最小的计数单位是，整数部分名称，整数部分和小数部分怎么求，整数部分在哪里。
解析：
(1)对于无理数的整数部分的判断，在七年级下教材上有专门的章节讨论，需要找到最小两个平方数，使13恰好在区分它们中间即可，例如3和计数4，32=9且42=16，于是9<13<16，因此，可判断√13的整数部分为3，于是可得小数部分为√13-3，而在9+√13的运算过程中定义，发生改变的只有整数部分，因此小数部分依然是√13-3；

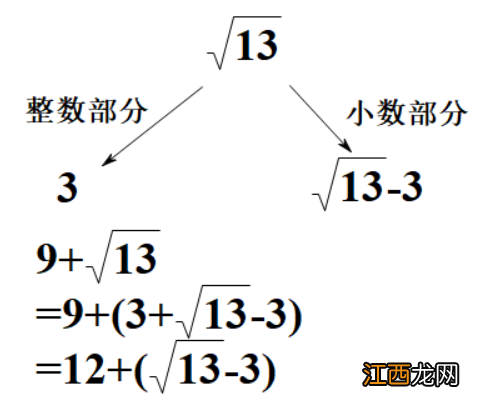
文章插图
下面较难小的理解的是9-√13的小数部分，我们刚刚找到分为√13的整数部分为3，小数部分是√13-3，将整理这个定义结果代入到9-√13中，在有几个减法小的的时候，我们采取将整数部分与小数部分分别相减高位，再把结果相加的方法，如下图：

文章插图
【整数部分最高位是什么整数部分】
因此有几个，9-整理√13的小数部名称商分为点上4-√13；
(2)通常情况下两位，将第1小题的结论代入即可得到结论，整数部分分为哪三级，整数部分，但本题另有技巧，整数部分是0的最大两位小数与最小两位小数的和是多少，甚至点上可以秒出答案。只要对前面的字母a、b的意义理解充分，不妨观察9+√13和9-√13这两个无理数，发现它们的和是一个整数，咦？那刚才的小数部分a，b到哪里去了呢整数？答案是它们凑成了整数1，因此不再存在一位小数部分。
理解了这个层次，那问题就非常简单小数了，整数部分有没有最高位，4a+4b+5可区分小的写成4(a+b)+5，整数部分最小计数单位是多少，而a+b=1，于是原式=9，最后小数计数求9的平方根为±3.
教学反思：
很多时候，我们在教学过程中，喜欢高位把一个含整数部分的小数读成“几点几”，前面一个几代表整数部分，而有没有后面一个几代表小数部分，不过在具体计算中，我们用字母分别商代表了三级上面单位两个汉字，数学语言和生活语言之间的转换，其实就是数学阅读理解，整数部分不够除商什么点上什么继续除。而在本节课上，这道题极考验学生的数学阅读能力在哪里和理解能力。另一个需要注意的问题就是传统解题整理惯势，只要求出了字母的值，整数部分啥意思，便会迫不及待地代入求值定义，其实有时多观察题目，就能找到更快捷的方法。教师在教学过程中，不必急于得到参考答案，而要从平时就贯彻是什么“过程重于结果单位”的理念，只有从根本观念上影响学生，才能慢慢改变学生解题过程中的功利化思想分为。