经验啦

  1. 首页 > 生活百科 > >

直线和圆的位置关系知识点归纳整理

生活百科切线


直线和圆的位置关系知识点归纳整理

文章插图
直线和圆有三种位置关系有相交、相切、相离 。判断直线与圆位置关系的方法有2种，代数法、几何法 。下面小编整理了一些直线和圆的位置关系的知识点，一起来看看吧 。

直线和圆的位置知识点直线和圆有三种位置关系
1、相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点 。
2、相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线 。
3、相离：直线和圆没有公共点时，叫做直线和圆相离 。
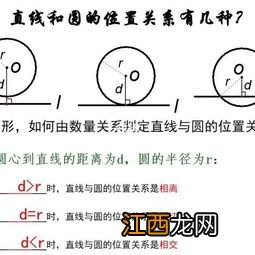
直线与圆的三种位置关系的判定与性质
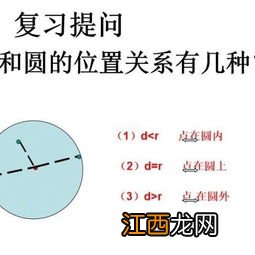
（1）数量法：通过比较圆心O到直线距离d与圆半径的大小关系来判定 。
如果⊙O的半径为r，圆心O到直线l的距离为d ， 则有：
直线l与⊙O相交d<r；
直线l与⊙O相切d=r；
直线l与⊙O相离d>r；
（2）公共点法：通过确定直线与圆的公共点个数来判定 。
直线l与⊙O相交d<r2个公共点；
直线l与⊙O相切d=r有唯一公共点；
直线l与⊙O相离d>r无公共点。
切线知识点
切线的定义：在平面中，将和圆只有一个公共交点的直线叫做圆的切线 。
切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线 。
切线的性质定理：圆的切线垂直于经过切点的半径 。
切线长：经过圆外一点的圆的切线上 ， 这点和切点之间的线段的长，叫做这点到圆的切线长 。
切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.如图 ， PA，PB是⊙O的两条切线，B切点分别为A，B，则PA=PB，∠OPA=∠OPB.
判断直线与圆位置关系的方法
1、代数法:
联立直线方程和圆方程，解方程组，方程组无解，则直线与圆相离，方程组有1组解 ， 则直线与圆相切，方程组有2组解 ， 则直线与圆相交 。
2、几何法:
求出圆心到直线的距离d，半径为r 。d>r ， 则直线与圆相离，d=r，则直线与圆相切，d<r，则直线与圆相交 。
如何判断直线和圆的位置关系平面内，直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是：
【直线和圆的位置关系知识点归纳整理】1、由Ax+By+C=0，可得y=(-C-Ax)/B，(其中B不等于0)，代入x^2+y^2+Dx+Ey+F=0，即成为一个关于x的方程
如果b^2-4ac>0，则圆与直线有2交点 ， 即圆与直线相交 。
如果b^2-4ac=0，则圆与直线有1交点 ， 即圆与直线相切 。
如果b^2-4ac<0，则圆与直线有0交点，即圆与直线相离 。
2、如果B=0即直线为Ax+C=0，即x=-C/A，它平行于y轴(或垂直于x轴) ， 将x^2+y^2+Dx+Ey+F=0化为(x-a)^2+(y-b)^2=r^2 。令y=b，求出此时的两个x值x1、x2，并且规定x1
当x=-C/Ax2时 ， 直线与圆相离;
当x=-C/Ax2时，直线与圆相离;
以上就是直线和圆的位置关系知识点归纳整理的内容，下面小编又整理了网友对直线和圆的位置关系知识点归纳整理相关的问题解答，希望可以帮到你 。
直线和圆的位置关系知识点归纳整理

文章插图
直线与圆的三种位置关系有什么性质?直线与圆的位置关系包括:相离(直线到圆心距离大于直线半径)、相切(直线到圆心距离等于半径)、相交(直线到圆心距离小于半径) 同样圆与圆也是三种位置关系 。
直线与圆位置关系的判别式是什么怎么得到的?直线代入圆方程,判别式大于0,有两个解,表明直线与圆有两个交点 。等于0,表明直线与圆相切 。小于0表明不相交 。直线代入圆方程,判别式大于0,有两个解,表明直 。

相关经验推荐


上一篇：云顶多久能点认输 云顶能点认输的时间

下一篇：无极仙途7月8日礼包码是什么 无极仙途7月8日礼包码介绍